全文包括:
SEM简介:功能、优点、缺点分析软件简介统计知识回顾:矩阵标量向量、多元回归分析、估计方法SEM的六大步骤路径追踪规则(Path tracing rules)R codes一、SEM简介强大的功能:
融合了因子分析(Factor Analysis)、方差分析(如ANOVA, ANCOVA, MANOVA, MANCOVA)、多重回归(multiple regression)等:
可以分析有多个因变量的模型(multiple dependent variables)可以分析复杂的中介模型(complex mediating mechanisms)可以估算潜在变量以解释测量误差(estimate latent variables)可以估算二分变量(binary) /序级变量(ordinal)的潜在因子可以测试跨组的模型不变性(test invariance of models across groups)可以建模重复测量的数据的发展轨迹(growth trajectories of repeated measures)不胜枚举的优点们:可以一次性完成对一个复杂模型的分析,而不用将模型拆分适用于各种数据(不同分布的数据-非正态分布,不同类型的数据-非连续数据)对长期数据sem结构方程模型步骤,可以测试个体的稳定性以及不足:建了个太太太复杂的模型,以致于啥都说明不了(比如把各种变量一股脑塞进模型,偏离了理论)—— 所以在建模specification/re-specification时,一定要明确自己在做什么,让模型保持精简。难以判断模型是否正好拟合(fit)数据 —— 要依据理论再参考一些fit index,将模型不断优化,在过度适合和适合不足中找到平衡点。可能有不同模型恰好一样地拟合数据没有明确参考标准来确定合适的样本大小——……样本量越大越好和其他分析一样sem结构方程模型步骤,SEM无法修正由于取样或测量导致的误差——好好设计和实施实验让数据质量高一些哲学盲点:SEM使用”证据的缺失(absent of evidence)作为支持假设模型的证据 —— 没有证据证明其存在可以证明其不存吗?(例一:研制新药,如果没有证据显示新药有疗效,是不是就能说明新药没有疗效了呢?例二:寻找某物种,如果找不到这个物种的生物,是不是就说明该物种已经灭绝了饿呢?)二、应用软件
常用软件:Amos(绘制路径图,简易模型分析,想发表文章的话还是用后两个分析吧)、Mplus(代码简洁好上手)、R(一般用lavaan package,还有别的包可以用比如semTools有一些补充功能比如求测量不变性 measurementInvariance(),semplot/lavaanplot可以用来绘图,还有openMX、sem等)。
除此以外,还有Python(学好编程啥问题都能解决)、LISREL(输入input是矩阵而非原数据!Coursera上有港中文大学Kit Tai Hau 侯傑泰教授的免费公开课程“Structural Equation Model and its Applications | 结构方程模型及其应用 (普通话/粤语))、EQS(多变量分析软件)、SPSS(也得自己码代码syntax,点点点鼠标是点不出来这些比较高级的功能的)。
三、统计知识回顾矩阵代数(Matrix Algebra)
标量(scalars):实数,只有大小,没有方向。

*a是一个标量,b也是一个标量。
矩阵(matrix):双序排列的标量,行(rows)+列(columns)。
*表示矩阵的字母一般大写、加粗。
矩阵排序:下标前面的数字代表行i,后面的数字代表列j,记作aij。

矩阵转置(Transpose):把矩阵A(r×c)的行和列互相交换,得到矩阵A’(c×r)。

对称矩阵(Symmetric Matrices):A = A’。
对角矩阵(diagonal matrix):特殊的对称矩阵,主对角线之外的元素皆为0的矩阵。
单位矩阵(Identity Matrix):特殊的对角矩阵,主对角线为1,主对角线之外的元素皆为0的矩阵。
向量(Vector):仅有一列/一行的矩阵。

*代表向量的字母一般小写加粗。
矩阵的加减乘除(我省略了)
但要注意的是,
行列式(Determinant)
多元回归分析(Multiple Regression)估计方法
最小二乘估计(Least Squares Estimation, LSE)
选择可以最小化残差的平方和(sum of squared residuals)的参数
最大似然估计(Maximum Likelihood Estimation, MLE)
频率学派(Frequentist)的点估计法,根据样本数据不断尝试,选出能最优描述实际概率分布(likelihood)的参数。
最大后验估计(Maximum A Posteriori Estimate, MAP)
提到了频率学派,就插入一下贝叶斯学派(Bayesian)的最大后验估计MAP。MAP融合了预估计量的先验分布信息(Prior distribution),对未观测点做估计,可以看作是正则化(regularized)的最大似然估计。
四、SEM操作步骤1. Specification 明确模型
自变量(independent variable)是什么?因变量(dependent variable)是什么?有没有调节变量(mediator)?有没有中介变量(moderator)?变量间是什么关系(relationship)?
1.1 路径图(path diagram)
路径图中图形的含义
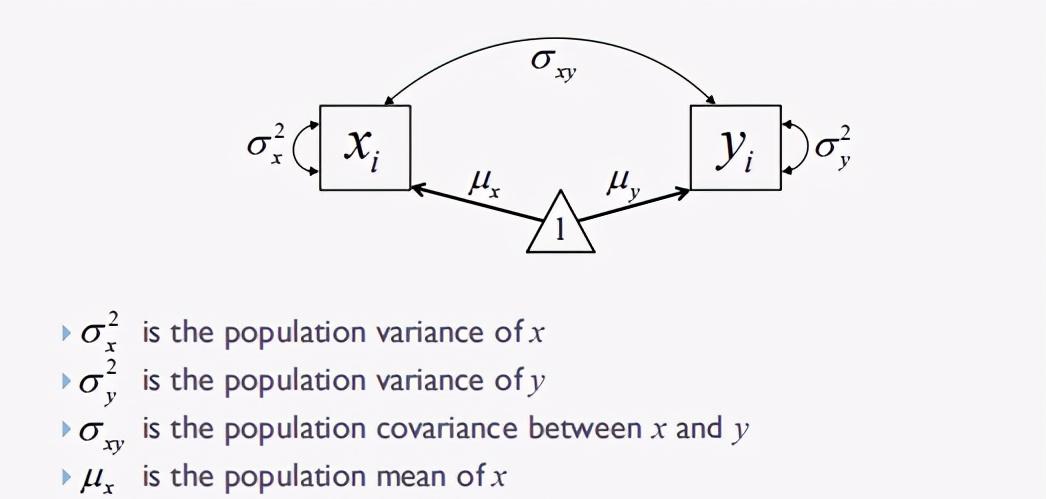
1.2 矩阵结构(Moment Structures)
如下图,以总体矩阵为例:对于单个因变量和q个自变量的回归模型,有一个总体的协方差矩阵Σ和总体均值向量μ。

2. Identification模型的辨识性
就像每个人都有个身份证号一样,一个模型需要具有辨识度。模型辨识度指的在有足够的已知信息来推断未知参数的程度。
Model identification refers to the extent to which there is sufficient known information to infer unknown values
许多路径分析和几乎所有SEM模型存在这个问题。
所有多元回归模型都是恰好识别。
大问题!无法得到有效结果,下面讲到的路径追踪规则(path tracing rules)对解决这个问题有用。
3. Estimate 模型参数估计
从样本数据中得到系数的过程。
3.1 最常用的是上述ML(最大似然法maximum likelihood),其具有3个特点:
a.无偏的:虽然每次都有抽样误差(sampling error), 但无限次重复实验后,样本估值的平均值将等于总体的真实值
unbiased: if we were to repeat our study an infinite number of times, the mean of the sample estimates would equal the population value
b.一致性:当样本量无限接近于总人群量时,样本估值也无限接近群体值
consistent: as the sample size approaches infinity, the sample estimate approaches the population value
c.有效性:参数估值的误差最小
efficient: no other estimator has a smaller sampling error for the parameter estimate
3.2 两种方式:
a. 充分统计最大似然值估计(Sufficient-statistic maximum likelihood estimation,SSML)仅仅基于观测到的协方差矩阵和均值向量,前提是有完整数据 (complete-case data)和正态分布的因变量(normally distributed DVs)
b. 完全信息最大似然值估计(Full information maximum likelihood estimator,FIML) 基于任何从个体观察到的数据。允许部分缺失的数据(partially missing data)和用于处理非正态分布(non-normal distribution)和嵌套数据结构( nested data structures)的替代方法
*对于完整的正态分布的数据,SSML 和FIML 一样。
3.3 优点:
3.4 步骤
初始值(start value):选择参数估计的初始值迭代(iteration):计算似然值,更新参数估计值收敛(converge):不断计算似然值,直到前后两个似然值之间的差异足够小为止从最后一步保留拟合值(Fit statistics)、参数估值(parameter estimates)和标准误差(standard errors )
*如果模型太复杂有可能出现模型不收敛“failed to converge”的问题。
4. Evaluation 模型评估
模型拟合程度如何?根据模型拟合指数作判断(Model fit index)
5. Potential re-specification可能需要模型再明确
如果模型不够好,怎么修改?参考理论,根据修正指数(Modification indices)调整模型。
6. Interpretation 解读
哪个结果显著?结果是否有意义?
限 时 特 惠:本站每日持续更新海量各大内部创业教程,一年会员只需98元,会员全站资源免费获取点击查看会员权益
站 长 微 信:ryenlii666


