一、因子分析模型
因子分析的目的主要是为了决定哪一组显变量具有相同的方差-协方差,从而用来构造理论上的概念、构想或因子(construct or factor),或潜变量(很多学者也常使用因子分析法来对数据进行降维)。事实上,Spearman(1904,1927)发明因子分析法,最初就是用来测量“智商”的。
因子分析可以分为探索性因子分析EFA和验证性因子分析CFA。验证性因子分析就是要收集显变量的数据,然后验证某一特定组的显变量能否用于构造某一个概念或因子;而探索性因子分析则判断是哪一些显变量与哪一个潜变量相关,有几个潜变量。
在验证性因子模型CFA中,研究者首先界定了一组因子、因子间相关关系以及测量每一个因子的显变量。也就是说,研究者已事先搭建了一个设定好的理论模型。接下来就是要检验一个理论因子模型的统计显著性,即样本数据能否验证该因子模型。在EFA中,会有多个不同的模型,最终要找到能拟合数据并具有理论支撑的模型。研究者需要探索这些变量能构造多少个因子、因子之间是否相关(如何相关),能测量这些因子的显变量是哪一些。因此,研究者事先并没有一个设计好的理论模型。
通常,验证性因子分析也被称为理论驱动研究(theory-driven),而探索性因子分析又被称为数据驱动研究(data-driven)。EFA适合理论尚未发展丰富的研究课题的数据分析,或不需要采用理论观点作指引的调查研究。从研究的角度来看,EFA和CFA具有相辅相成的功效(Coste et al., 2005)。
二、常用的因子分析法
主成分因子分析PCFA是最常用的因子分析法(因为它是很多统计软件默认的因子分析法),但很多学者指出PCFA远非最好的因子分析法,甚至根本就不是一种因子分析法。PCFA的缺陷在于,它试图解释一组指标变量的全部方差或协方差(total variance),而不是这些指标共同或共有的协方差(shared or common variance)。也就是说,PCFA假设每一个指标变量都没有各自的独特方差或误差方差(只有共性,没有个性)。事实上,Stata也提供了多种其它更好的验证性因子分析法,包括极大似然因子分析(maximum likelihood factor analysis)。而结构方程模型因子分析法(测量模型)则是一种比其它传统方法更好的因子分析法。
假设用x1-x10共10个指标去测量保守度(Conservatism)。各个指标变量的取值为1-4,如下表所示:
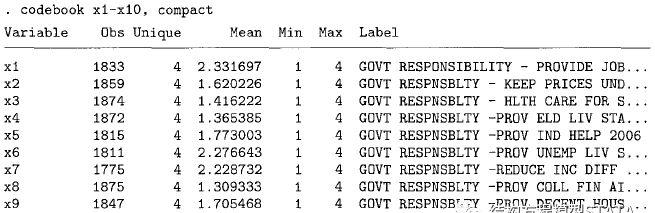
主成分因子分析法的命令如下:factor x1-x10, pcf
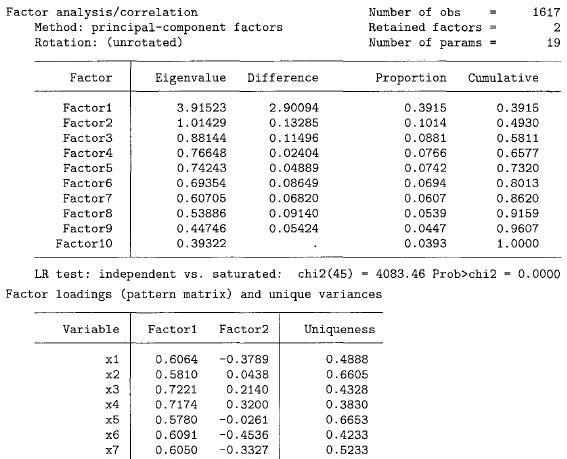
PCFA使用的是相关系数矩阵,因而会将每一个指标标准化(方差为1)。因此,10个指标的特征值加总等于10。而通常认为当特征值小于1时,该因子就不宜采用。上表所得到的结果中,只有2个因子的特征值大于1。
特征值指的是该因子在多大程度上能解释全部指标的总方差?特征值等于各个因子中各指标因子载荷的平方和。第一个因子有一个很强的特征值(eigenvalue)3.92。3.92意味着第一个因子能解释这些指标39.2%的方差。计算如下:
.6064^2+.5810^2+.7221^2+.7174^2+.5780^2+.6091^2+.6050^2+.5994^2+.7330^2+.4543^2=3.92
在上表中,只有因子1是较强的因子(strong factor),也符合只需构造一个因子的目的。同时,因子1各个指标的因子载荷也全部大于0.4。0.4是接受一个指标测量某因子的通常标准。Costello & Osborne(2005)则认为0.3是接受一个指标变量的最低标准,即该指标对因子的因子载荷不能少于0.3。事实上,因子载荷就是指标变量与因子之间的相关系数。
表中还报告了每一个指标的独特值(uniqueness)。这个独特值代表了每一个指标的独特方差或误差的方差。例如,x1的方差中有61.03%没有被该因子所解释。然而,PCFA因子法往往假设这些独特方差都为0。由于这些独特方差都比较大,显然是不能轻易被忽视的,而应该采用其它的因子分析法去考虑它们的影响。例如,主因子法(principle factor method)在处理时就不会假设这些独特方差值为0。命令为:
factor x1-x9, pf
下一步就是计算这九个指标的信度系数,具体使用alpha命令。命令如下:
alpha x1-x9, item label asis
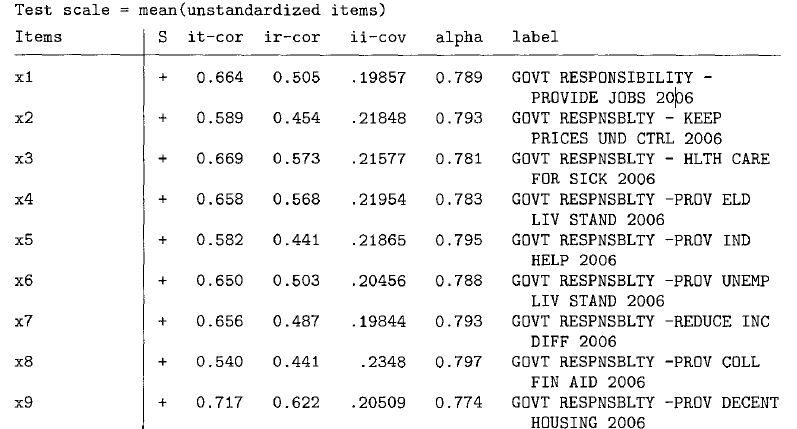
在上表中的最下行,信度系数为0.81,超过0.7的最低标准。表中的alpha列表示如果去掉这一个指标,alpha将变为多少。如果去掉一个指标能增加alpha值,也要认真检查该指标是不是与其它指标一样确实是在衡量同一因子。
三、SEM估计因子模型
不同于PCFA,其它因子分析法允许每一个指标都有独特的方差,并且假设这些误差项服从正态分布,且序列不相关。
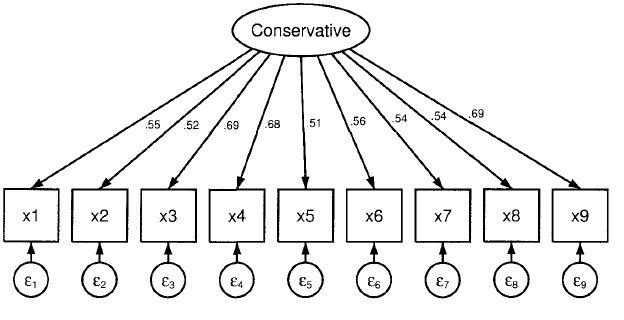
下图中,因子(潜变量)代表了一组显变量的共同变化/方差(common variation)。该因子解释了被访者如何回答或响应各个指标变量。单箭头代表了因子及其显变量(测量指标)之间的关系。其中sem结构方程模型图,因子是解释变量,指标为被解释变量。这是因为对指标的回答结果取决于因子的水平(取值)。二者的相关性也被称为因子载荷(factor loading),而因子载荷的平方又被称为变量的公共(共性)值(commonality estimate)。
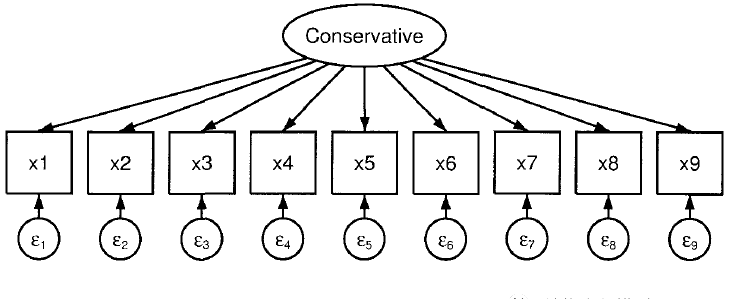
测量误差则被置入椭圆形之内。测量误差代表了该显变量自己独有的变化(unique variation),这种变化与所测量的因子无关。也就是说,该显变量除了测量模型中的公因子之外,还有一部分是在测量别的特征——另一个不同的因子或测量误差(unreliability),又被称为误差因子或特殊因子(易丹辉,2008)。为反映测量误差的大小,模型会基于样本数据估计出每一个测量误差的方差(measurement error variance)。即模型假设9个指标的方差(协方差)能被一个单因子加上各自独特方差所解释。而PCFA则假设该因子就可以解释全部的方差,而不需各自独特的误差方差。
SEM的CFA方法具有更多的优点。将九个指标共有的方差与各自独特方差分隔开来,能获得对潜变量更好的测量结果。通过消除潜变量的测量误差(measurement error),当这些潜变量在结构方程模型中被用作解释变量或被解释变量时,可以获得更优的估计结果(strong results)。这是因为测量误差本质上只是给测量结果带来无用的噪音,本身并没有任何的解释力(explanatory power)。
使用结构方程模型的CFA方法估计上图的单因子CFA模型。命令如下:
sem (Conservative -> x1-x9)
所用的估计方法为极大似然估计法,最大化对数似然函数(log-likelihoodfunction)。估计结果如下:

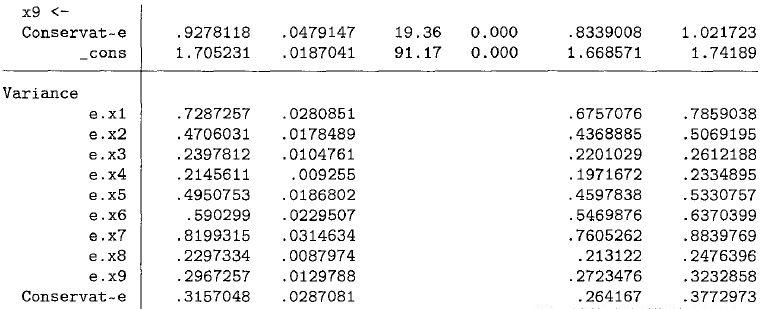
估计结果由两栏构成,一栏为测量模型,报告非标准化的测量系数(因子载荷)、标准误,95%置信区间、z检验值。而PCFA方法仅估计并报告因子载荷。
第二栏是误差项的方差估计值。系数列报告了非标准化的载荷系数。为计算潜变量的方差sem结构方程模型图,Stata程序将第一个指标的系数固定为等于1。这个指标也被称为参照指标(reference indiator)。而如果更改了新的参照指标,则所有的非标准化系数估计值也会一起改变。为此,建议使用最强的指标做为基准指标(系数最大的指标)。如果要更改默认的第一个指标,则只需将该指标变量放到第一的位置就可以了。
为获得标准化估计结果(显变量和潜变量的方差设为1),可以使用命令:sem (Conservative ->x2 x1 x3-x9),standardized,或在估计结束后,输入命令:sem,standardized。图形如下所示:
限 时 特 惠:本站每日持续更新海量各大内部创业教程,一年会员只需98元,会员全站资源免费获取点击查看会员权益
站 长 微 信:ryenlii666


